
BUAA_OO 第三单元:社交网络(JML) 总结

前言
第三单元主题是JML,但在我看来也是两个维度的考量,一是对JML的学习,这个我觉得更多体现在实验课需要我们写JML,以及通过读懂JML来知道我们三次迭代需要实现的函数的功能是什么;第二个维度就是依托于社交网络这么一个主题,在图论中的算法上做出了一些考察,如果不优化算法的话,大概率会在强测中就出问题
因此本人的第三单元总结分为两部分,第一部分是我对JML的认知理解,这一部分只是浅谈,因为真没什么好谈的,老生常谈,陈词滥调;第二部分是我三次迭代中一些好的设计,其中第二次迭代里globalTags的设计是我觉得最具有创新性的,也解决了我的燃眉之急
其实这里就可以简单谈一谈U3算法层面的事,其实我有感知到课程组更多的希望我们在这一单元学会的是JML,因此都删除掉了性能分。但很多人卷的方向都是效率,可能是受限于10s的CPU运行时间,同时后面又发生了本地和测评机因环境不同导致的测评误差,我个人简单认为可以适当的放缓测评机的测评压力或者提供一个模拟测评机高并发测评时的环境供我们课下的时候进行测试,以及指导书中只是指出了CPU时间限制为10s,但并未表明CPU的具体参数或者说具体的环境,这一点我也是存疑的。
但是但是,我的代码貌似并没有涉及到CTLE的问题,对不起,确实是效率上卷的有点多,不过整个U3除了让我知道了JML这个东西意外,巩固了图论中的一些算法,最大的收获是有了对于社交网络这个业务场景的一些考量。我很多的设计都遵顼:用空间换时间、动态维护做到o(1)的查询复杂度这样的原则,可能同样一个对象会存储在很多的容器中,满足不同方式的查找,所以后续迭代部分会具体讲解我的设计以及考量
第一次作业分析
任务简析
实现用户类Person、社交网络类Network和四个异常类,重点在于按照JML的规格实现方法。
如果直接按照JML来翻译,不优化算法的话,大概率会在互测阶段被hack掉,所以后文依托于方法的实现来介绍本人的设计。
具体实现
第一次作业的方法可以分为两类:创建形(add、modify等)、查询形(query等),本人的主要策略是动态维护network中的各种关系,使得查询时尽可能是 o(1) 的复杂度,这就会增加时间成本以及内存占用,需要注意不要堆溢出。
Person
在network中的persons我使用HashMap来维护,HashMap在哈希冲突不严重的时候是靠链表来处理冲突,严重之后会自动转为红黑树,在我看来person的查询可以控制在 o(logn) 是可以接受的。故MyPerson类中的acquaintance与value容器也是使用HashMap来维护(第二次迭代中又增加了acquaintanceSort起到排序的作用)
Relation
最后三个查询性质的函数都与person之间的关系有关:isCircle 、queryBlockSum 、queryTripleSum,从图论的角度来翻译:isCircle 是两个点是否具有连通性;queryBlockSum 是图中极大连通子图(连通分量)的个数;queryTripleSum 是图中二度正则子图的个数。
针对前两个函数,我使用的方法是改良的并查集:
新建一个类DisjointSet来负责维护network中所有person的连通性:
1 | public class DisjointSet { |
其中涉及到了并查集算法中的路径压缩以及按秩合并,同时维护了一个blockNum变量来记录连通分量数,这样前两个函数就迎刃而解了
不过其中还涉及到一个问题就是 modifyRelation 方法可能会删除两个人的关系,我们知道朴素的并查集是不支持删除操作了,这里我的处理方法是在遇到需要删除边的时候重建并查集(本人是重建整个并查集,事实上只需要重建删除边的那一个连通子图就好了,本人懒得再去优化了,干脆一刀切),具体的实现方法如下:
1 | //DisjointSet.java |
其中还设置了一个脏位disjointSetNeedReset,在删除边且需要查询的时候再重建并查集
至于最后一个函数queryTripleSum,我没有想到特别好的方法,比起需要查询的时候到persons数组中遍历,大概是o(n^2)甚至是o(n^3)的复杂度,我依旧选择动态维护tripleSum这一变量:
1 | //MyNetwork.java |
因为新增一个三角形只会因为新增一条边(删除同理),故可以提取出person1的acquaintance,查询person2是否也与之相连,可以在o(m)的时间复杂度下判断新增三角形个数。
以上的动态维护思维实际上是牺牲了维护的成本,比如上面的维护三角形个数,可能全局的查询三角形个数的指令只有一条,但是每当addRelation或modifyRelation时就需要更新一下tripleSum,这个问题在我看来关键是取舍,设计的问题本身就没有最优解,只有权衡。
第二次作业分析
任务简析
这次迭代的跨度应该是三次中最难的,增加了标签类MyTag,同时针对value这一属性增加了关系之间的查询
故我将新增的需要实现的方法分两类:
- addTag、delTag、addPersonToTag、delPersonFromTag、queryTagValueSum、queryTagAgeVar
- queryBestAcquaintance、queryCoupleSum、queryShortestPath
可以看出,第一类都是和Tag有关,而第二类更多的是依托于Acquaintance这一Person的属性
具体实现
Tag
我对tag的特殊处理有两处,第一处是针对于person1所拥有的所有Tag,我建立了一个tagsCatch的机制来快速判断另外一个person2是否属于person1的某些Tag中:
1 | //MyPerson.java |
这个优化是一个很小的优化,甚至我现在看来维护成本可能都大于它带来的优化收益,其作用是在modifyRelation时如果要删除两人的关系,那么可以o(1)的时间复杂度下得到person1所有的Tag中哪些含有person2,进而再去删除关系。
第二处我看来是特别好的一个优化,因为解决了我们想要动态维护ValueSum这一Tag中的属性的问题:
首先对于Tag中的需要查询的属性:valueSum和ageVar,我起初的想法是加入或删除一个Person后就更改这两个属性的值,再查询的时候直接返回,可以做到 o(1) 的查询效率,但是后来发现value这一属性的可以通过modifyRelation来改变的,而找到person1和person2共同处于的Tag不是一件容易的事(因为我们存储Tag的结构是person所含有的Tag,而不是person所处于的Tag)
故我反其道而行之,空间换时间的思想做到机制,在MyNetwork设置了globalTags这一容器记录person所处于的Tags这一信息:
1 | //MyNetwork.java |
在addRelation和modifyRelation的时候调用changeTagValue改变person1和person2共同所处的Tags的valueSum,addPersonToTag等维护方法保持不变。
这么做要注意globalTags的维护,addPersonToTag、delPersonFromTag、delTag、addTag 、addPerson、 modifyRelation都需要对globalTags 做维护,这样子的处理下,维护一次valueSum的时间复杂度应该是 o(m),当然,相较于现查询现计算valueSum的o(n^2),是我能接受的程度。
根据后期和其他同学比较时间,我的代码虽然做不到最快,但和最快的同学也相差不多,这源自于指令的侧重点,如果全文都是关系的维护指令,那我这种维护成本很高的设计模式就会败下阵来;但如果查询指令居多的话,我的代码还是很占据优势的。不过思考下来,可以设置脏位来平衡维护和查询的关系,靠脏位来判断,需要维护且需要查询后再去维护(我懒啦)。
Acquaintance
queryBestAcquaintance、queryCoupleSum这两个指令关联性比较强,coupleSum可以依托于bestAcquaintance来计算。queryBestAcquaintance的处理是在Person类里维护Acquaintance数组的顺序:
1 | //MyPerson.java |
利用TreeSet的排序的特性,只需要更改比较回调函数,就可以完成排序的行为。为什么是新增acquaintanceSort而不是对原来的HashMap做更改?其实也是空间换时间的考量,不想舍弃最优 o(1) 的查询速率(也可以用TreeSet的contains,但不如HashMap效率好)
不过这样子也是增加了维护成本,给person增加一个acquaintance需要维护两个容器,同时这里我还犯了一个重大的、经典的bug,先放一张图,在后面bug分析里再做赘述:
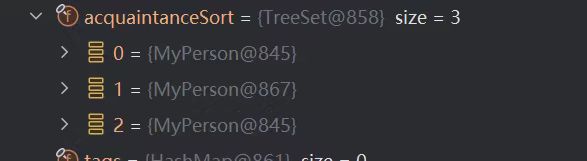
TreeSet中出现了两个地址一摸一样的对象?(并没有更改equals方法)
至于queryCoupleSum则是采取 o(n) 复杂度的现查现算,因为o(n)我还是能接受的(其实就是懒了,懒得再去维护啦哈哈)。遍历persons,查看person1的bestId(person2)的bestId是不是person1,记得result要除以2呀
最后queryShortestPath这个函数只是使用了一个简单的BFS做处理,因为前面用来维护的容器大都是一维的,但是最短路径维护需要二维,而且处理起来依托于算法,我认为BFS就够用,而且可以结合并查集,先判断连通性,这里就不赘述BFS的写法了,很板子
第三次作业分析
任务简析
实现Message有关的操作,Message具有三个继承于他的子类,Message存在于network和person中
总体来感知第三次迭代的难度很低,相比于第一次作业的并查集、第二次作业很多动态维护的处理、第三次迭代并未有值得提及的设计,基本都是朴素的翻译JML实现,不过第三次作业的JML确实难读,需要有很好的耐心,故下面就未有具体实现啦
bug分析
TreeSet
针对上面那个TreeSet出现两个相同的对象的问题,这里做解释:
当时我的acquaintanceSort的维护是这么处理的:
1 | //MyPerson.java |
我已经标出了问题行数,因为当一个acquaintance的value发生改变,他在TreeSet里的顺序也该发生改变,我处理的方法是将它remove掉后再add,但是这样子就犯了一个很经典的问题,我们不妨就利用上面的MyPerson@845为例子,例如原本845位于MyPerson@867的左子节点(即845在我的比较算法下小于867),我们现在先更改845的属性,使得845大于了867,那么TreeSet的remove函数就只会去867的右分支上去寻找845,显然是找不到的,然后再add845也是添加到右分支上,这时867的左右子节点就都是845了,两者是一个对象,究其根本是不应该直接更改树结构对象的属性。
我后续的补救措施就是将15、16行代码更换顺序,先找到要更改属性的对象,将它从TreeSet中删除,再去更改属性,再去加入到树中,这样子可以规避上面的问题,是安全的(当然我不确定,TreeSet中可能有更好的内置处理方法),总之这个bug很经典,值得引以为戒
改写compare
1 | //MyPerson.java |
这是我原本的改写compare方法的写法,10行犯了很经典很严重的错误,就是会爆int,即可能发生**int_max - (int_min)**这种情况, 其实归根结底是书写习惯不好造成的,这种改写比较回调函数,应该不嫌麻烦,用if-else然后return 0、1、-1,或者像我上面一样调用java.Integer自带的compare方法(一样的),总之这个问题也很致命,一般的测评还真测不出来,但架不住强测里有助教ggjj们造出来的极端数据
浅谈JML
到目前为止我对JML的感觉还是:无感。
硬要为它正名的话,他比自然语言更具有完备性,能够更准确的表述某个方法或某个类需要满足的要求与功能,同时更利于junit测试代码的书写。但同时它也会带来很大的学习成本,以及读懂一个JML并不难,因为我们三次迭代的需求都是读懂官方给的JML,但是如果让我来写一个方法的JML,我不敢保证我写的规格是完备的。
所以不能说是完全没有收获
Junit测试
黑箱测试与白箱测试
- 黑箱测试:黑箱测试强调输入和输出之间的关系,而不关注内部实现。对于我们自己搭建的测评机,采用对拍来判断正确性,即是黑箱测试
- 白箱测试:白箱测试则更注重代码的覆盖率。可通过分析代码,利用IDEA中已有的覆盖率分析来进行测试
单元测试、功能测试、集成测试、压力测试、回归测试
- 单元测试:单元测试是最基础的测试方法,针对每个类和方法进行了独立的验证。通过JUnit框架,课程组三次作业中要求我们对三次作业中的三个函数进行单元测试
- 功能测试:功能测试注重整个系统的功能性,通过模拟实际使用场景来验证系统的完整性。例如,第二次迭代中Tag部分的功能和BestAcquaintance部分的功能无关,可以选择只针对其中一方面做高强度的测试。
- 集成测试:集成测试旨在验证各模块之间的协作性。在本单元中,特别是社交网络和用户类之间的交互,需要进行集成测试。
- 压力测试:为了验证系统在高负载情况下的表现,可以设计了压力测试。例如在本地模拟了大量用户和关系的数据,通过JVM监控工具观察内存和CPU的使用情况。重点测试了在大量关系和频繁修改情况下,系统的响应时间和稳定性。
- 回归测试:回归测试用于验证修改后的代码没有引入新的错误。在每次提交新的代码后,运行之前的所有测试用例,确保新功能的添加或Bug的修复不会破坏现有功能。
数据构造策略
- 随机数据生成:通过编写随机数据生成器,模拟实际使用中的各种情况。
- 边界数据测试:设计极端情况的数据,例如最大和最小值,以验证系统的稳定性,这个在第二次作业中由于我的懒惰疏忽了这种测试数据的引入,导致compare改写出错。
- 预定义数据集:手动编写一些特定场景下的数据,确保特殊情况下系统能正确处理。
JUnit与规格
在设计JUnit测试时,充分利用JML规格信息。通过对JML的详细解读,确定每个方法的前置条件和后置条件,编写相应的测试用例。例如,在测试deleteColdEmoji方法时,在测试代码调用完这个方法后,重点验证所有的后置条件是否满足,而不可只关注返回值是否正确。
总结
总体的体感还是不错的,并没有前两单元那么高压,同时也有这一单元的亮点。
我觉得这一单元不止学习JML,而还需要涉及图论方面的算法,以及降低时间复杂度的考量,这点是很棒的,算是这一单元的难点与挑战,我认为这一层次的考量甚至可以大大方方的写入指导书中
- 标题: BUAA_OO 第三单元:社交网络(JML) 总结
- 作者: rainbowYao
- 创建于 : 2024-07-03 21:18:08
- 更新于 : 2024-09-18 09:28:36
- 链接: https://redefine.ohevan.com/2024/07/03/BUAA-OO-第三单元:社交网络(JML)-总结/
- 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。



