BUAA_OO 第一单元：表达式展开总结

前言

OO正课第一单元的主题是表达式展开，主要训练层次化设计，本单元经历了三次迭代，层层增加难度，目的是让我们可以设计出好的架构，应对新增要求时可以尽量少的做更改以维持架构的不变。

本文分别介绍三次迭代分析，每部分包括任务简析、代码UML类图、架构分析、具体实现过程、其他方面、自动化测评，然后是最终版本的复杂度分析，最后是包含三次迭代中的bug分析

以下代码仅为部分示例代码，全部代码（程序源码、测评机）已上传github个人仓库

第一次作业分析

任务简析

本次作业是展开一个最多嵌套一层括号的单变量多项式，多项式中项的因子只能是常数因子、幂函数因子、表达式因子，最后在正确展开的前提下再比较表达式的长度。

主线任务：

解析字符串
展开有括号的表达式，得到一个多项式
化简多项式并输出

代码UML类图

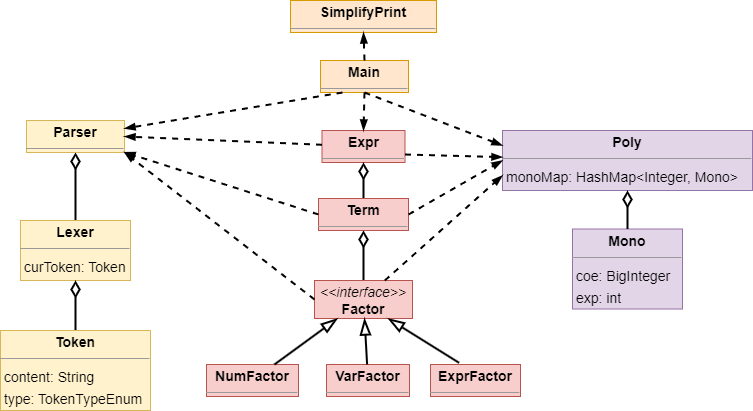
架构分析

架构大致分为三个横向的组织：文法分析(Parser, Lexer)，表达式结构(Expr, Term, Factor)，多项式运算(Poly, Mono)
大致步骤就是先用parser解析表达式，然后再在每一个元素中都加上转化成Poly类的方法。在Poly类中实现多项式相乘相加的方法。在Expr.toPloy()中，实现所包含的Term.Poly()的相加；在Term.toPoly()中实现所包含的Factor.toPloy()的相乘(也是一个递归的过程)。

具体实现过程

分成三个主要步骤：表达式解析（递归下降法）、表达式展开和表达式输出

表达式解析：递归下降法

预处理

在预处理阶段我主要做了两件事情：

将输入字符串中的所有空白字符替换为空串。
删除前导“+”，合并重复运算符（如-+-替换成+）。

解析

具体的方法（递归下降法）在oolens的推送以及训练题中有详细介绍，在这里我仅提一下我的一些特殊的处理：

在处理token流时去除数字前导0。这里就不给具体实现了，很好做
容错性输出。在一些程序不应该进入的部分设置一些特定输出，利于debug

else {	
    System.out.println("Dont know what to do with " + input.charAt(i));
  
else {
    System.out.println("pos is more than token list");

项之间可能是由+或者-号连接的，oolens给出的方法是在Expr类中存储这种排列的信息，但是我感觉这样做的话不太美观，在处理时也会变得更加复杂。所以我们不妨在这里认为项之间全都是相加的关系，而-的存储则由Term类和Factor类负责，设置为Term和Factor的一个属性。

  public Expr parserExpr() {
      int signal = 1;
      if (lexer.notEnd() && lexer.getCurToken().getType() == TokenTypeEnum.SUB) {
          signal = -1;
          lexer.move();
      }
      terms.add(parserTerm(signal));
…………          

表达式展开：处理多项式

具体实现

表达式展开的思路我主要是参考了一位学长的博客（hyggge学长），他是在Expr,Term,Factor中都实现了toPoly()方法，并在Poly类中实现了addPoly(),multiPoly(),powerPoly()方法。这里的toPoly() 方法：

对于NumFactor与VarFactor，转化为仅含有一个Mono对象的Poly
对于ExprFactor,我们假设此时已经实现了expr.toPoly()，那么可以先后使用expr.toPoly()与 powerPoly
对于Term, 仅需使用multiPoly将Factor调用toPoly()的结果乘起来即可
对于Expr, 仅需使用addPoly将Term调用toPoly()的结果加起来即可
此处仅给出Term 的 toPoly 为示例：

public Poly toPloy() {
    Poly poly = new Poly();
    poly.addMono(new Mono(BigInteger.ONE, 0));
    for (Factor factor : factors) {
        poly = Poly.multiPoly(poly, factor.toPloy());
    }
    if (signal == -1) {
        Poly.negatePoly(poly);
    }
    return poly;
}

这个方法中，hyggge学长抓住了题目的核心需求（让我们输出由若干x的n次幂相加组成的多项式），有基本项的概念，此处的基本项是：$Poly = \sum Mono, Mono = a * x ^b$。这使得代码的可扩展性变得十分高，即使是以后新增其他东西（比如三角函数、指数函数、多变量、自定义函数）也是完全适用的。

细节处理

多项式HashMap的键值映射我当时有两种选择：“指数——系数”、“指数——单项式”，虽然后者与前者功能完全相同且为了获得系数还需要调用mono.getCoe() 方法，但这么处理是为了以后迭代预留可扩展的空间，此处的Mono可看成基本项，这样提取键值即可得到基本项的全部属性

private final HashMap<Integer, Mono> monoMap;

通过静态方法传两个参数进入addPoly(),multiPoly(),powerPoly()，规避深浅拷贝的问题，在静态方法里面新建一个Poly对象返回

public static Poly addPoly(Poly poly1, Poly poly2) {
    Poly poly = new Poly();

    for (Integer exp: poly1.getMonoMap().keySet()) {
        poly.addMono(new Mono(poly1.getMonoMap().get(exp).getCoe(), exp));
    }

表达式输出：化简表达式

上述过程没有bug的话，我们会得到一个符合如下格式的多项式：$$\sum_1^ncoex^{exp}$$。其中的指数不会相同，因为在addPoly中就可以实现*同类项合并

优化有以下几点：

指数为0、1，系数为-1、+1、0时可化简输出
删除coe为0的项，但当Poly中monoMap被删空时（即表达式本身是0的情况），向其中加入一个0，这里也别忘记用迭代器去删除
由于会出现-x+1比1-x长的情况，因此这一步需要改变输出顺序使得第一项尽可能为正

其他方面

打包工作

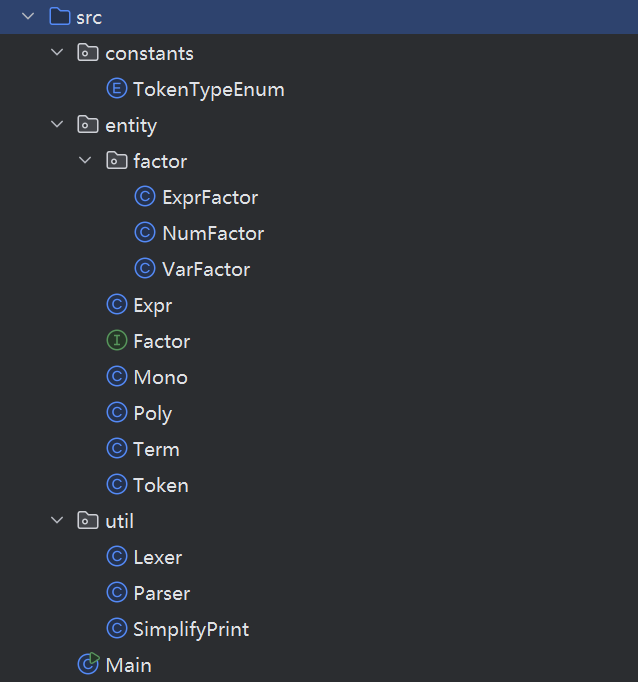
本人代码习惯之一是会在编程开始前打包：utils、entity、constants、config四个基本的包

utils：顾名思义就是工具类、其中类的方法大多为静态方法（从业务角度，我们不需要有两个Parser对象，或者说创造出两个Parser对象，他们处理的也是同一业务逻辑）。从目的来看，utils类能解决代码复用问题。

entity：实体类，里面放置的一般是业务主体，也就是需要频繁创造出新对象的类

constants：常量类，定义项目中的常量，如正则表达式、枚举类等

config：全局配置类，对项目对象做到统一管理（OOp 中本人就设置了Adventurers类，将其静态化，使得全局都可以调用到”冒险者集合“，不过这种操作要考虑过度暴露的风险）

基于接口而非实现编程

实际上，“基于接口而非实现编程”这条原则的另一个表述方式，是“基于抽象而非实现编程”。好的设计一定是：越抽象、越顶层、越脱离具体某一实现的设计，越能提高代码的灵活性，越能应对未来的需求变化

本人觉得接口的特性是面向对象编程最具优势的特性，它像是一种”协议“，规定了只暴露给上层哪些信息，不关心具体实现。

factor接口暴露给上层一个方法：

public Poly toPloy();

即将Factor转化成Poly（后续我会讲基本项，此处的Poly可短暂的看成第一次作业的基本项），故无论有多少种类的因子，在上层（Poly、Mono）的眼中，只关注下层factor会传递给他一个什么样的Poly，而不关注其具体实现。故在后续增量迭代中，我们只需要考虑新增的factor要如何转化为Poly、而不影响上层代码的结构。

“基于接口而非实现编程”这条原则，不仅仅可以指导非常细节的编程开发，还能指导更加上层的架构设计、系统设计等。（这是理论上讲的后话，本人也未曾实践）

Poly、Mono的引入，单一职责

这段主要讨论下第二部分的设计优势，由于有了基本项的概念，第二部分的代码逻辑（poly类、mono类）我个人觉得可以完全不涉及化简部分、只实现将递归下降解析出来的AST语法树转化为基本项集合，再将基本项集合传递给第三部分化简输出工序，这样设计的好处是以后的增量迭代中只需要关注：新增的要求满足什么样的基本项，而无需关注形式（即化简的部分），第二部分（Poly、Mono，以后可能就不这么命名了）中代码功能仅是转化为基本项集合， SimplifyPrint 的代码功能再去考虑基本集合中是否可以合并化简，满足SOLID原则中的单一职责原则。

改写toString方法

虽然上文讲过第二部分仅处理基本项的转化，但我的Mono类中有改写toString方法：

    @Override
    public String toString() {
        if (exp == 0) {
            return coe.toString();
        } else if (exp == 1) {
            if (coe.equals(BigInteger.ZERO)) {
                return "";
            } else if (coe.equals(BigInteger.ONE)) {
                return "x";
…………

这时候就有问题，那这么做是不是违背了单一职责原则，我觉得并不然：设计的问题本身就没有最优解，只有权衡。为了使用方便，我们只能做一些妥协

如果将toString方法放到SimplifyPrint类中只会加剧这个类的处理逻辑复杂度，而且归根结底SimplifyPrint是会与Mono类有耦合，相比将Mono传递进SimplifyPrint后再做处理，不如直接传递给SimplifyPrint Mono的最简输出，这样做反而会一定程度的降低Mono和SimplifyPrint的耦合度

自动化测评

相关python代码和操作可以看 oolens 发的推送以及b站学长录制的视频，其中我的数据生成器主要是翻译题目的BNF，通过python中的random库控制数据难度，其中通过传入 deepNum 参数控制括号仅可嵌套一层

def g_expr(deepNum):
    termNum = random.randint(1, 3)
    result = g_whitespace() + g_add_sub() + g_term(deepNum) + g_whitespace()

    for i in range(termNum - 1):
        if random.random() < 0.5:
            result = result + g_whitespace() + '+' + g_whitespace() + g_term(deepNum)
        else:
            result = result + g_whitespace() + '-' + g_whitespace() + g_term(deepNum)            
    return result

测评器中是用python中的sympy库对数据生成器产生的样例和样例经过jar包运行输出的答案进行化简后比对，其中有两个小细节：

sympy中的simplify() 方法无法处理前导0
比对可以不从字符串相等层面上比对，sympy提供了许多方法来处理表达式之间的关系，如equals(other)：检查两个表达式是否在逻辑上相等。

data_no_leading_zero = re.sub(r'\b0+(\d+)', r'\1', data).replace(" ", '')

expr1_simplified = simplify(sympify(data_no_leading_zero))
expr2_simplified = simplify(sympify(result))

expressions_equal = expr1_simplified.equals(expr2_simplified)

第二次作业分析

任务简析

本次作业新增难度分两点：自定义函数、指数函数（exp）

主线任务：

解析支持自定义函数（比较重要）和指数函数
展开计算中考量基本项是什么
化简方法如何增加

代码UML类图

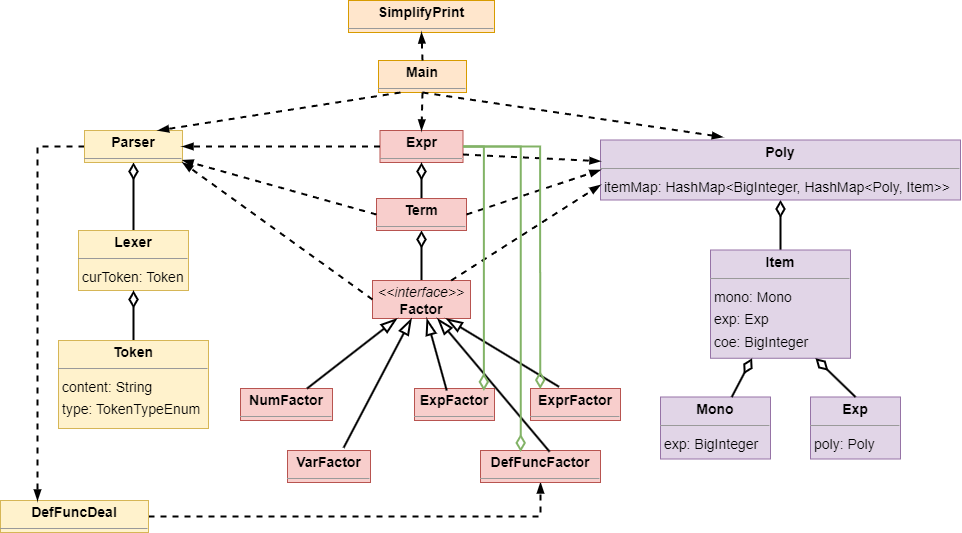
架构分析（只讨论新增）

沿用之前架构，在文法分析中加入DefFuncDeal类去替换解析自定义函数，表达式结构中加入了ExpFactor DefFuncFactor实现Factor接口，多项式运算结构改变，新增Item类为基本项、Item 由 Mono 和Exp 组合
解题顺序上不变，新增的步骤是在解析表达式Expr expr = parser.parserExpr() 的过程中通过 private Factor parserDefFuncFactor(int signal) 解析自定义函数；Poly 的计算方法因基本项改变和指数函数的加入而做适当调整；输出化简类做调整。

具体实现过程

只从三方面讨论：自定义函数替换策略、Poly基本项处理、可行化简方法

自定义函数替换策略

本人当前自定义函数的处理采用的是字符串层面的替换（思路也来自于hyggge学长的博客），即递归调用toString方法（后续其他细节上会讲到还可以从AST语法树的层面做替换，即递归调用toPoly方法，需要者可提前前往）。

首先是自定义函数因子类 DefFuncFactor 的处理，部分代码如下：

//DefFuncFactor.java
    private final String calledFunc;
    private final Expr expr;

    public DefFuncFactor(String name, ArrayList<Factor> actualParas) {
        this.calledFunc = DefFuncDeal.callDefFunc(name, actualParas);
        this.expr = dealExpr();
    }

    private Expr dealToExpr() 
}

//DefFuncDeal.java
    private static final HashMap<String, String> funcMap = new HashMap<>();
    private static final HashMap<String, ArrayList<String>> formalParasMap = new HashMap<>();

    public static void addDefFunc(String input) //函数名与形式化表达式存在funcMap中

    public static String callDefFunc(String name,  ArrayList<Factor> actualParas) {
				...//形参实参对应
				...//调用lexer解析形式化表达式为token流
        while (lexer.notEnd()) {
            if (lexer.getCurToken().getType() == TokenTypeEnum.Var) {
                Factor factor = parasMap.get(lexer.getCurToken().getContent());
                sb.append(factor.toString());     //toString方法实现字符串层面上的替换
            } else ……

属性上：calledFunc 顾名思义是被调用后的函数表达式（字符串形式），其实它算是一个中间变量，亦可不设置属性存储它；expr 则是将替换后的函数表达式解析成AST语法树的形式，存在expr中，此时DefFuncFactor 某种程度上等价于指数是1的 ExprFactor

方法上：函数调用通过工具类 DefFuncDeal 实现，该工具类中两个静态方法 addDefFunc 在终端将函数名与形式化表达式之间建立映射；callDefFunc 先建立形参实参的映射，然后进行替换（这里建议用token流处理，后面会讲）替换则是直接调用factor的 toString 方法，之后返回字符串层面的已经替换好了的表达式，回到DefFuncFactor 中再通过 dealToExpr 实现calledFunc 转化成 expr，实际上也只是在此调用parser、lexer解析表达式

细节处理：

为了规避exp中的x 被理解成形式参数替换为实参，本人不采用遍历字符串的方法，而是将形式表达式通过lexer分析成token流（这说明我的lexer中将x、y、z都设定成了TokenTypeEnum.Var），可见上面代码
递归调用toString时注意加括号保护。想这么一个例子，$f(x) = 3x, f(f((x+1)))$ ，如果DefFuncFactor 的toString 方法没有给转化出来的表达式外层套括号，会转化成$33*(x+1)$，而正确的转化应该是$3*(3*(x+1))$，本人实现factor接口的类中还有符号signal这一属性，为了规避字符串替换后曲解语义或违背词法的情况，我大都添加了括号（后续讲到AST语法树层面的替换时可很好的规避这些问题）

Poly基本项处理

很多人都想到了本次作业合并同类项化简的点在于如何判断exp的指数相同，我当时有两种选择，一个是将exp的指数看成表达式expr，可这样就要改写所有AST语法树类的equals、HashCode 方法且很容易犯错（如误判x+1和1+x不相等）；第二个方法是将exp的指数算成基本项的形式，递归定义基本项，因为基本项经过自己的程序计算后应该有唯一形式、这样也可以边比较exp的指数是否相同边计算，如下：

本人本次作业定义的基本项如下形式：$Item = coe * x^{exp} *e^{Poly}$ , $Poly = \sum Item$,其中Poly 类的属性是一个HashMap的嵌套，通过两个指数exp和Poly二维索引到coe（也可以索引整个Item，目的是合并同类项）；Item 的属性则是coe、Mono 、Exp，即它的系数和两个指数（两个指数我封装成了两个类，Exp是指数函数，exp是变量x的指数，目的是后续可以分层次书写toString方法）

//Poly.java
    private final HashMap<Integer, HashMap<Poly, Item>> itemMap;
//Item.java
    private BigInteger coe;
    private final Mono mono;
    private final Exp exp;
//Exp.java
    private final Poly poly;
//Mono.java
    private final int exp;

故关注点在于AST语法树类如何实现toPoly方法和Poly 中 add、multi等计算方法如何更改。

首先我想第一个难点是如何定义0，对于Poly，当itemMap.isEmpty() 时我规定他是0，定义了函数public boolean isZero()，后续化简输出的时候先调用这个函数。而后续新建Item类时，如果没有exp部分，则其exp中的Poly传递一个新创造的Poly即可，这样子递归定义的Poly基本项形式就有了递归终点。
其次计算方法上的更改有许多细节上与hw_1不同，如addItem 函数中，通过两层索引找到两个指数都相同的项，若系数相加合并后为0，则要去除这一hash键值对，而不是简单将系数设为0，如果mono的指数索引不到任何exp的指数（前面定义的0也包含），也要删除这一键值对，原因是我们前面定义的0是不含任何项的itemMap

//public void addItem(Item item)
	if (newCoe.equals(BigInteger.ZERO)) {
		itemMap.get(exp).remove(poly);
		if (itemMap.get(exp).isEmpty()) {
			itemMap.remove(exp);
		} 
  } else {
    	existingItem.setCoe(newCoe);
	}

基本项乘法multiPoly中要实现两个指数函数系数的相加，即：Poly newPoly = Poly.addPoly(item1.getExp().getPoly(),item2.getExp().getPoly());，这里调用了addPoly 此处的addPoly一定要深克隆出item1和item2的poly，即：

//addPoly        
        for (Integer exp: srcPoly.getItemMap().keySet()) {
            for (Poly tempPoly : srcPoly.getItemMap().get(exp).keySet()) {
                Item item = srcPoly.getItemMap().get(exp).get(tempPoly);
                Item newItem = new Item(item.getCoe(), item.getMono(), item.getExp());
                destPoly.addItem(newItem);
            }
        }

否则返回newPoly中item的Poly的地址是item1或item2的Poly (此处会在最后bug分析时再次赘述)

既然有了Poly类中的计算方法，只需依次实现AST语法树类的toPoly 方法就可以实现将expr转化成上面递归定义的基本项，此处仅给出一个：

//expr.java    
    public Poly toPoly() {
        Poly poly = new Poly(); //这就是0啊！！！
        for (Term term : terms) {
            poly = Poly.addPoly(poly, term.toPoly());
        }
        return poly;
    }

可行化简方法

本人将可以想到的化简方法一次列举下：

指数0、1，系数0，1，-1的输出化简：这部分的话我写在了Poly、Item 等基本项类中，通过改写他们的toString 方法化简输出，如：
依旧沿用hw_1的思路，多项式相加时放一个正项在前面（我写在了SimplifyPrint类中，我的Poly 的toString 方法就是调用了 SimplifyPrint类中的方法，所以exp指数部分的Poly转化输出时是最简形式，这也是递归调用）
针对指数函数的特殊处理，如exp((2*x)) 要比 exp(x)^2 多一个字符，提取公因数放到指数部分会更短，甚至一个exp可以拆成两个exp相乘（这部分可见其他分享贴子的陈述，本人只做到对于多项式提取相同的系数放在指数上，如exp(3*x^2+(x+2)^2) 结果会是exp((x^2+x+1))^4，会比标准形式 exp((4*x^2+4*x+4))短）

其他方面

清洗代码

既然都开始迭代了，有的代码段要增量，不防从头到尾给自己的代码来一遍清洗，改掉之前代码风格或编程方式不好的地方。

手动清洗

如将功能逻辑平行的代码拆成内部的静态函数，下面是在解析因子时（我第一次是写在一个大的函数里）

//parser.java中的parserFactor()
				if (lexer.notEnd() && lexer.getCurToken().getType() == TokenTypeEnum.NUM) {
            return parserNumFactor(signal);
        } else if (lexer.notEnd() && lexer.getCurToken().getType() == TokenTypeEnum.Var) {
            return parserVarFactor(signal);
        }………………

    		private Factor parserNumFactor(int signal)
    		private Factor parserVarFactor(int signal)

重复操作建立映射，如我第一次作业处理token流的时候读到“()+-*”等的处理逻辑是一样的，但我写了5个类似的if，这次又增加了新的元素，不妨建立一个映射，这样子可以只写一个if。

//lexer.java
		tokenList.add(new Token(content, TokenMap.TOKEN_MAP.get(content)));

//TokenMap.java  
    public static final Map<String, TokenTypeEnum> TOKEN_MAP =
        Map.of("(", TokenTypeEnum.LP,
                   ")", TokenTypeEnum.RP,
                   "+", TokenTypeEnum.ADD,

相同或类似功能的代码段提取出来封装成一个函数，类似功能是指功能有一点点差异，可以通过传入参数做选择，如下

 public boolean hasOneItemOfType(boolean baseItem) {
……
     for (Integer exp : itemMap.keySet()) {
         for (Poly tempPoly : itemMap.get(exp).keySet()) {
             if (baseItem && itemMap.get(exp).get(tempPoly).isBaseItem()) {  //此处是base
……								
             } else if (!baseItem && itemMap.get(exp).get(tempPoly).isNormalItem()) {  //此处是Normal
……	

chatgpt清洗

这个工作完全是可以交给chatgpt来处理的，当然他不一定能满足你的要求，我们只取其精华，取其糟粕，如我它提示我可以做如下替换：

  if (c == "(" || c == ")" || ………………)

private boolean isBaseToken(char ch) {
      String baseTokens = "()+-*^xyz,";
      return baseTokens.indexOf(ch) != -1;
  }

AST语法树层面的自定义函数解析方法

本人未使用这种方法，但经过思考觉得是一种可行解，而且比字符串层面的替换更具优点，故此处只提供思路：

同样是建立自变量因子类 DefFuncFactor ，其中存的也是一课语法树，即expr，但其中的形参与实参不做替换，只做对应映射关系的存储（这就要求语法解析部分可以解析y、z）
在DefFuncFactor 的 toPoly的方法中做特殊处理，即算到形参的时候不调用形参的toPoly方法，而是实参的toPoly方法（这也要求形参是一个实现了Factor接口的类）
这样做就将字符串层面的替换转化成了Poly值的替换，好处是不需要在乎字符串层面的特殊处理，性能上也会更有，再有就是更符合结构化，这样做的考量才是真正将自定义函数看成一个因子，而字符串层面的替换本质上是将自定义函数看成另外四种因子的组合。
这段文字书写于撰写以上文字的后一天，这一天间隔里都在干嘛？debug！总结出来的结论就是字符串层面的替换真的是一不小心就会出错，而学过编译的某人讲说“AST语法树层面的替换是gcc最佳实践”，我深有所感
第三次作业重构了使用了这种方法、其中再做赘述

自动化测评

整体框架没有变，因为需要解析自定义函数，所以选取了讨论区的一种方式：exec()方法

测评机代码也已上传github

第三次作业分析

前情提要：hw_2结束后更改了解析自定义函数的方法，看过我上次经验分享的人应该知道有字符串层面的替换和语法树层面的替换，这次更改成语法树层面替换的考量后续会赘述

任务简析

本次作业新增要求仅为：求导因子

主线任务：

解析求导因子
支持求导计算

代码UML类图

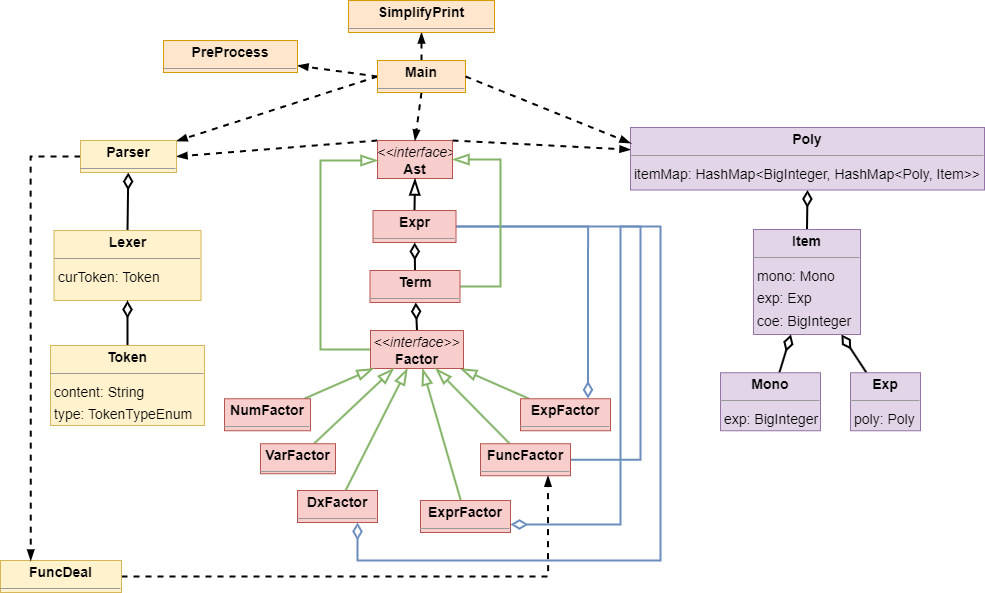
架构分析（只讨论新增）

因为解析表达式的原因，本人新增ast接口，让语法树解析类全部实现此接口，实现formalParaReplace 和 toPoly 两个函数（主要是统一了toPoly方法）
新增DxFactor，相当于是存储了一个表达式的因子，只是后续其toPoly 方法要做求导处理
PreProcess 预处理单独提取成一个工具类，血的教训

具体实现过程

这里只讲求导的处理，自定义函数处理方法的更改写在其他细节里

求导处理

本人在预判了第三次新增功能是求导的前提下，认为第二次的架构是十分合理的，相比对表达式求导，我们回看对基本项的求导就有很公式化的做法:

$$dx(Poly) = dx(\sum Item) = dx(\sum ax^{b}e^{Poly}) = \sum (abx^{b-1}e^{Poly} + dx(Poly)ax^be^{Poly})$$

可以看出来只要实现了Poly的求导算法（类似于addPoly 、multiPoly 等），就可以实现将求导因子展开，且算出的结果也是基本项Poly的形式

//DxFactor.java
	private final Expr expr;
	private final int signal;
	public Poly toPoly() {
		Poly oriPoly = expr.toPoly();
		if (signal == -1) {
			Poly.negatePoly(oriPoly);
		}
		return Poly.derivatePoly(oriPoly);
	}

//Poly.java
	public static Poly derivatePoly(Poly poly) {
		for (BigInteger exp : poly.itemMap.keySet()) {
			for (Poly tempPoly : poly.itemMap.get(exp).keySet()) {
         Poly derItem = item.derivateItem();    //递归调用Item的求导，Item求导后的Poly相加即可
			}
		}
    …………
      
//Item.java
	public Poly derivateItem() {
		Poly result = new Poly();
			if (exp.getPoly().isZero() && mono.getExp().equals(BigInteger.ZERO)) 
			else if (exp.getPoly().isZero()) 
			else if (mono.getExp().equals(BigInteger.ZERO)) 
			else
………………   

求导因子作为ast解析语法树时的存储单位，其属性为一个expr 和 signal , 转化为poly 的时候，只需要将expr 转化为poly 再去调用 poly 求导方法，返回的仍是 poly

poly 求导就是基于求导法则，poly 相当于很多项item 的和，只需要调用item的求导，item 求导我又分为了只有系数、系数*x、系数*e、系数*x*e四种

其他方面

自定义函数替换策略更改

因为本次求导运算的处理是将表达式转换为poly再去运算，其实函数表达式的替换也可以看成是一种运算，而都通过toPoly来处理可以达到行为上的统一（这样做终于不用考虑字符串层面替换中嵌套括号做保护的“丑陋处理“了）

//FuncDeal.java    
    public static Expr callDefFunc(String name,  ArrayList<Factor> actualParas) {
        Expr expr = parser.parserExpr();
        expr.formalParaReplace(parasMap);

//ast.java
    public interface ast {
        void formalParaReplace(Map<String, Factor> map);
        Poly toPoly();

//VarFactor.java
    public VarFactor(String powerNum, int signal, boolean isFormalPara, String name) {
        this.isFormalPara = isFormalPara;
        this.factor = null;
   
    public Poly toPoly() {
        if (isFormalPara) {
            Poly factorPoly = factor.toPoly();
					 …………

    public void formalParaReplace(Map<String, Factor> map) {
        if (isFormalPara) {
            this.factor = map.get(name);

//Parser.java
    private final boolean isDealFunc;

首先 VarFactor 变量因子增加了isFormalPara 、name、 factor 三个属性，将其扩展成了形参x、y、z和实际计算中的x可公用的ast语法树存储结构，如果 isFormalPara 为真，则factor 存储他对应的实参，在 toPoly 的时候实现替换
那解析时就要区分是不是在解析函数表达式，故我为 Parser 增加了一个判断是不是在解析函数表达式的参数，为VarFactor 传递参数
同时我考虑到实参替换的时候需要遍历 Expr寻找VarFactor ，故实现 ast 接口的语法树类都实现其中的formalParaReplace 方法，深度遍历去寻找形参将其 factor 属性替换成实参
这样处理之后可以删除所有ast语法树类的toString 方法，做到行为上的统一

预处理方法封装出来

预处理操作原本是放在Lexer里的静态方法，但由于解析函数定义式（此处发生了特别愚蠢的bug，后面会赘述）时也需要用到，则将这一方法提出为一个单独的类的静态方法，这样更满足单一职责原则

自动化测评

测评正确性时不用sympy方法，而是使用对拍的方法，思路也来源于一篇讨论贴

debug总结

我的室友zyt 永远的神

此处按照时间顺序反省三次迭代中几个重要的大bug

深浅克隆

第一个大bug发生在第二次迭代，当时的Poly中的addPoly是将两个Poly的哈希表合并返回（使用的是put方法），这导致poly1和poly2相加完之后得到newPoly，三者哈希表中存的元素是相同的，一个改动，另外的两个也会被改动，导致bug，前面已经给出了更改后的代码。

忘记预处理

这是最微不足道但造成后果最严重的bug，导致我第二次作业强测寄掉，即没有对函数定义式做预处理，我函数定义式使用的是正则表达式匹配，其中并没有处理空格以及制表符，所以千里之堤、毁于蚁穴，故我将预处理提封装一个单独的工具类，因为它不只受用于 Lexer 。

依旧是深浅克隆，以及对AST语法树替换的预想

这里的深浅克隆指的是第三次迭代中AST语法树替换部分，在我为形参赋值实参的时候，所有实参都是直接从hashMap中取出来的，但由于第三次作业允许函数定义式中使用已经定义好的函数，就出现了形参的实参是形参的情况（想一下，虽然这么说很抽象），这导致赋值工作会出现很多问题，比如我的变量因子赋值实参的方法就很欠妥，类似于打补丁：

@Override
public void formalParaReplace(Map<String, Factor> map) {
    if (!isFormalPara) {
        return;
    }
    if (factor instanceof VarFactor) {
        if (!((VarFactor) factor).isFormalPara()) {
            return;
        }
    }
    if (factor == null) {
        this.factor = map.get(name).deepClone();
    } else {
        factor.formalParaReplace(map);
    }
}

其中如果不调用deepClone 的话就会出现问题（value_data 中含有有价值的样例，同步测评机上传github了），所以如果有人不用字符串替换而也选择这种方法的话，欢迎进行更好的优化

TLE优化

这个针对ltc 同学的神仙样例：

他巧妙地利用exp的代价函数不大的特性构造出了这么个嵌套了十多层exp的样例，我的代码跑这个样例5min都跑不出结果，我就利用了idea中自带的分析工具 IntelliJ Profiler 发现 hashcode 费时过大，因为我为了哈希表可以将两个内容一样的poly判定为相等，故改写了hashcode ，这个样例应该是会频繁的计算hashcode导致TLE，故我采用“缓存哈希码”的方法 (zyt用的ArrayList，靠他的一些手段也使得效率很高，可以研究下)：

private int cachedHashCode = 0;

@Override
public int hashCode() {
    if (cachedHashCode == 0) {
        cachedHashCode = Objects.hash(poly);
    }
    return cachedHashCode;
}

将5min都跑不出来的bug控制到了0.2s跑出（所以要善用性能分析工具）

这段话写于和ltc 同学交流，我想明白了使用HashMap改写hashCode等价于使用ArrayList改写equals方法（都是为了合并同类项时候判等地址不同、内容相同的poly），而要注意如果自己的设计会导致已经计算hashCode的poly会改变，那么要重新计算hashCode（我的架构规避了这个问题，当我需要计算得出一个新的poly时，我不会对已有poly做修改，而是新建一个poly，这样子可以保证hashCode是唯一的）

rainbowYao's Blog

BUAA_OO 第一单元：表达式展开 总结

前言

第一次作业分析

任务简析

代码UML类图

架构分析

具体实现过程

表达式解析：递归下降法

预处理

解析

表达式展开：处理多项式

具体实现

细节处理

表达式输出：化简表达式

其他方面

打包工作

基于接口而非实现编程

Poly、Mono的引入，单一职责

改写toString方法

自动化测评

第二次作业分析

任务简析

代码UML类图

架构分析（只讨论新增）

具体实现过程

自定义函数替换策略

Poly基本项处理

可行化简方法

其他方面

清洗代码

手动清洗

chatgpt清洗

AST语法树层面的自定义函数解析方法

自动化测评

第三次作业分析

任务简析

代码UML类图

架构分析（只讨论新增）

具体实现过程

求导处理

其他方面

自定义函数替换策略更改

预处理方法封装出来

自动化测评

debug总结

深浅克隆

忘记预处理

依旧是深浅克隆，以及对AST语法树替换的预想

TLE优化

BUAA_OO 第一单元：表达式展开总结